Difference between revisions of "Geodesic Temple"
| Line 4: | Line 4: | ||
Description: a modular, self-supported, burnable sculpture made of platonic solids.<BR> | Description: a modular, self-supported, burnable sculpture made of platonic solids.<BR> | ||
Octahedron<BR> | GeoTem 05 ([http://en.wikipedia.org/wiki/Octahedron Octahedron])<BR> | ||
[[File:GeoTem04plan.jpg|300px]] [[File:GeoTem04pers01.jpg|300px]] [[File: | [[File:GeoTem05plan.jpg|300px]] [[File:GeoTem05pers01.jpg|300px]] [[File:GeoTem05pers02.jpg|300px]] <BR> | ||
Height: 63 all octahedrons are the same size. is 91 feet tall. | |||
[http://en.wikipedia.org/wiki/Icosahedron Icosahedron]: a regular polyhedron with 20 identical equilateral triangular faces which is also a geodesic volume and a platonic solid.<BR> | |||
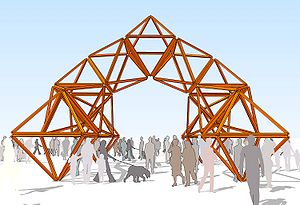
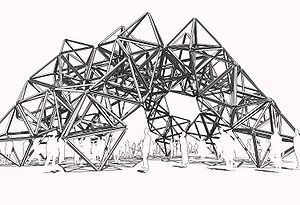
GeoTem 04 ([http://en.wikipedia.org/wiki/Octahedron Octahedron])<BR> | |||
[[File:GeoTem04plan.jpg|300px]] [[File:GeoTem04pers01.jpg|300px]] [[File:GeoTem04Octa01.jpg|300px]] <BR> | |||
[[Media:Geodesic_temple_2011.skp]]<BR> | [[Media:Geodesic_temple_2011.skp]]<BR> | ||
all icosahedrons are the same size and the sculpture is 91 feet tall. | all icosahedrons are the same size and the sculpture is 91 feet tall. | ||
[http://en.wikipedia.org/wiki/Icosahedron Icosahedron]: a regular polyhedron with 20 identical equilateral triangular faces which is also a geodesic volume and a platonic solid.<BR> | [http://en.wikipedia.org/wiki/Icosahedron Icosahedron]: a regular polyhedron with 20 identical equilateral triangular faces which is also a geodesic volume and a platonic solid.<BR> | ||
Icosahedron<BR> | GeoTem 01, 02 ([http://en.wikipedia.org/wiki/Icosahedron Icosahedron])<BR> | ||
[[File:Geodesic_temple_2011_03.jpg|500px]] [[File:Geodesic_temple_2011_04.jpg|500px]]<BR> | [[File:Geodesic_temple_2011_03.jpg|500px]] [[File:Geodesic_temple_2011_04.jpg|500px]]<BR> | ||
[[Media:Geodesic_temple_2011.skp]]<BR> | [[Media:Geodesic_temple_2011.skp]]<BR> | ||
all icosahedrons are the same size and the sculpture is 91 feet tall. | all icosahedrons are the same size and the sculpture is 91 feet tall. | ||
: a regular polyhedron with 20 identical equilateral triangular faces which is also a geodesic volume and a platonic solid.<BR> | |||
The Dex is covered with similar pieces.<BR> | The Dex is covered with similar pieces.<BR> | ||
Revision as of 09:11, 13 January 2011
Project for a burnable sculpture by Disorient in 2011
Presented at Burning Man, Coachella, Figment, Electric Zoo etc.
Description: a modular, self-supported, burnable sculpture made of platonic solids.
GeoTem 05 (Octahedron)
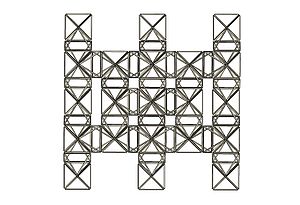
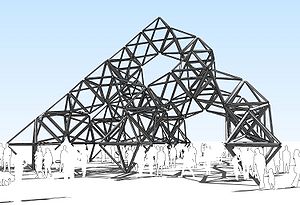
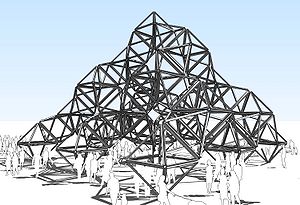
Height: 63 all octahedrons are the same size. is 91 feet tall.
Icosahedron: a regular polyhedron with 20 identical equilateral triangular faces which is also a geodesic volume and a platonic solid.
GeoTem 04 (Octahedron)
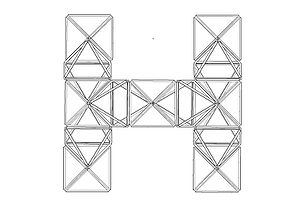
Media:Geodesic_temple_2011.skp
all icosahedrons are the same size and the sculpture is 91 feet tall.
Icosahedron: a regular polyhedron with 20 identical equilateral triangular faces which is also a geodesic volume and a platonic solid.
GeoTem 01, 02 (Icosahedron)


Media:Geodesic_temple_2011.skp
all icosahedrons are the same size and the sculpture is 91 feet tall.
- a regular polyhedron with 20 identical equilateral triangular faces which is also a geodesic volume and a platonic solid.
The Dex is covered with similar pieces.
Possible materials: wood, cardboard, paper...
Probable material: 2x4 wooden studs.
Lighting: multiple opportunities. Elements of new Leo Sign could be mounted on the struts. One strobe pointing inside each polyhedron.
Some elements are left free-standing on the ground so they can be moved/rolled by anyone to reconfigure the piece.
Skin: sides can be (partially) skinned individually. Skinning the structure would help with shade, burn and lighting but would create more resistance to wind which is a problem on the playa. Maybe only lower parts of the structure are skinned?
Dex transformation uses same polyhedron.
Camp frontage uses same polyhedron.
Funding:
- Apply for grants: Figment, Burning Man;
- Coachella, Electric Zoo
Notes:
- Loops help with structural integrity. How do we make loops using respective polyhedrons?
| <videoflash type="youtube">XbSmkNHScLg|450|337</videoflash> |


